Negli anni ’60, nei laboratori di calcolo scientifico, un piccolo dettaglio algoritmico avrebbe cambiato il modo in cui gli studiosi guardano ai numeri casuali. Quel dettaglio si chiamava RANDU, uno dei generatori di numeri pseudocasuali più diffusi… e più problematici della storia.
Che cos’è RANDU?
RANDU è un generatore lineare congruenziale, un algoritmo che produce sequenze di numeri apparentemente casuali secondo la formula:
$$X_{n+1} = (a \cdot X_{n} + c) \mod m$$
Nel caso specifico di RANDU, i parametri erano:
- a=65539
- m= $2^{31}$
- c= 0
Questo algoritmo era incorporato nei computer IBM e utilizzato in simulazioni Monte Carlo in fisica, ingegneria e statistica. Appariva efficiente e “casuale” a prima vista, tanto da guadagnarsi la fiducia di intere generazioni di scienziati.
Ma arriviamo alla ragione dello scandalo, i numeri che generava avevano davvero un comportamento pseudo-casuale?
Effettivamente se proviamo a generare un milione di numeri e facciamo l’istogramma, appare una distribuzione uniforme….
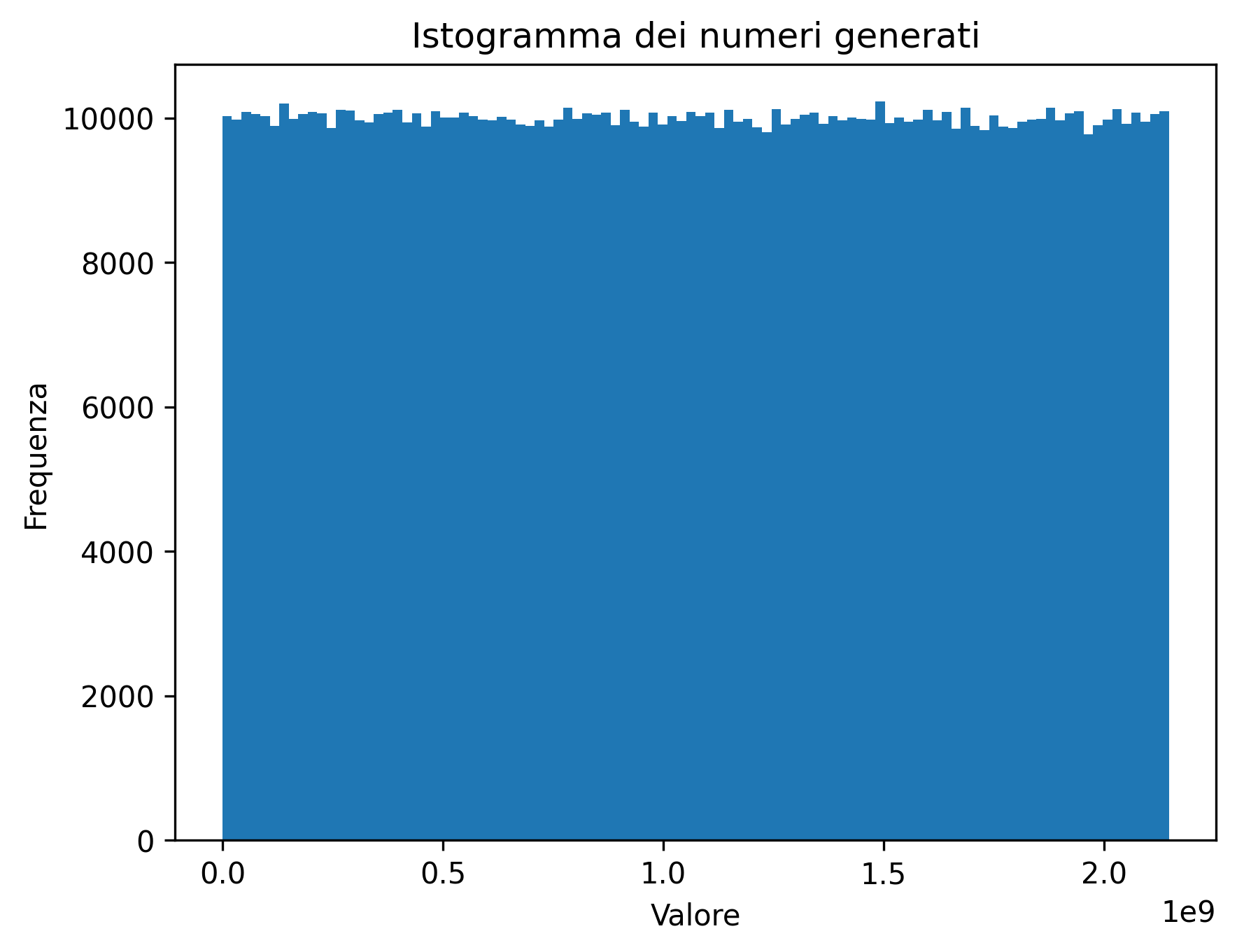
Proviamo a graficare in 3D i numeri generati da RANDU associandoli a triplette di punti cartesiani come in figura:

Anche se proviamo a graficare i numeri generati da RANDU separandoli in triple successive di numeri generati, prendendo: $(X_n,X_{n+1},X_{n+2})$ come $(x,y,z)$ il comportamento potrebbe comunque apparire corretto…
Infatti sembrerebbe ancora essere frutto di una distribuzione uniforme…
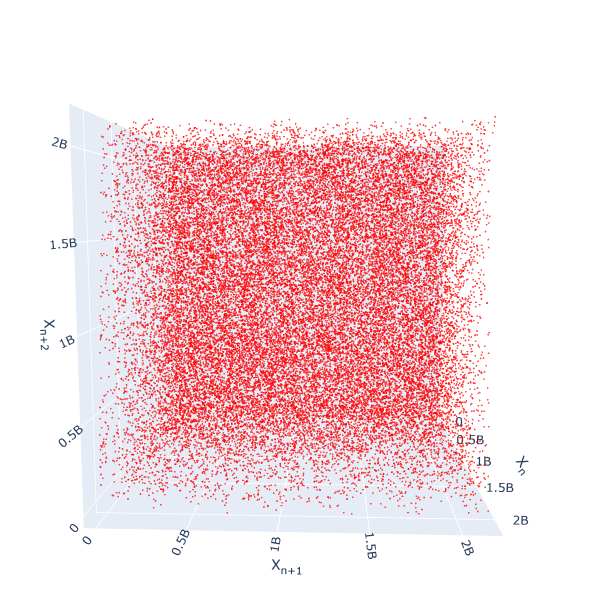
Ma attenzione… Ruotando leggermente l’immagine ci viene rivelato il problema:
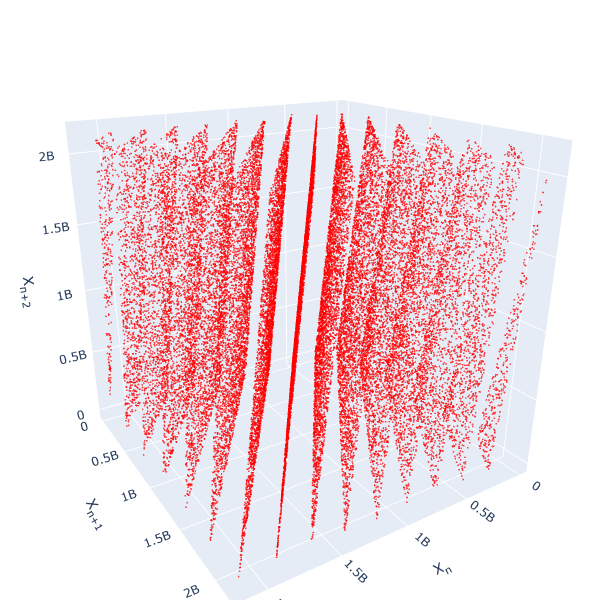
In uno spazio tridimensionale, i punti non si distribuiscono uniformemente come ci si aspetterebbe da una sequenza casuale, ma cadono su 15 piani distinti.
Questo fenomeno è dovuto a una scelta inadeguata dei parametri: la sequenza sembra casuale guardata singolarmente, ma le correlazioni tra numeri consecutivi introducono pattern regolari.
Il difetto di RANDU ha avuto effetti concreti: simulazioni Monte Carlo che si basavano su di esso potevano fornire risultati distorti e falsamente coerenti. In altre parole, la scienza stava interpretando come casuale ciò che in realtà era strutturato e prevedibile.
Questo non è solo un curioso aneddoto storico. È diventato un caso di studio classico sull’importanza di verificare la qualità dei generatori di numeri pseudocasuali prima di usarli in applicazioni critiche. Anche oggi, quando si progettano algoritmi per simulazioni, crittografia o intelligenza artificiale, il principio rimane lo stesso: un numero casuale mal progettato può compromettere interi esperimenti.