Tempo fa un amico mi ha proposto un problema di logica matematica davvero intrigante, e da allora non ho smesso di pensarci.
Immaginate un esagono composto da celle esagonali più piccole, il cui lato misura 5 celle (come mostrato in figura).
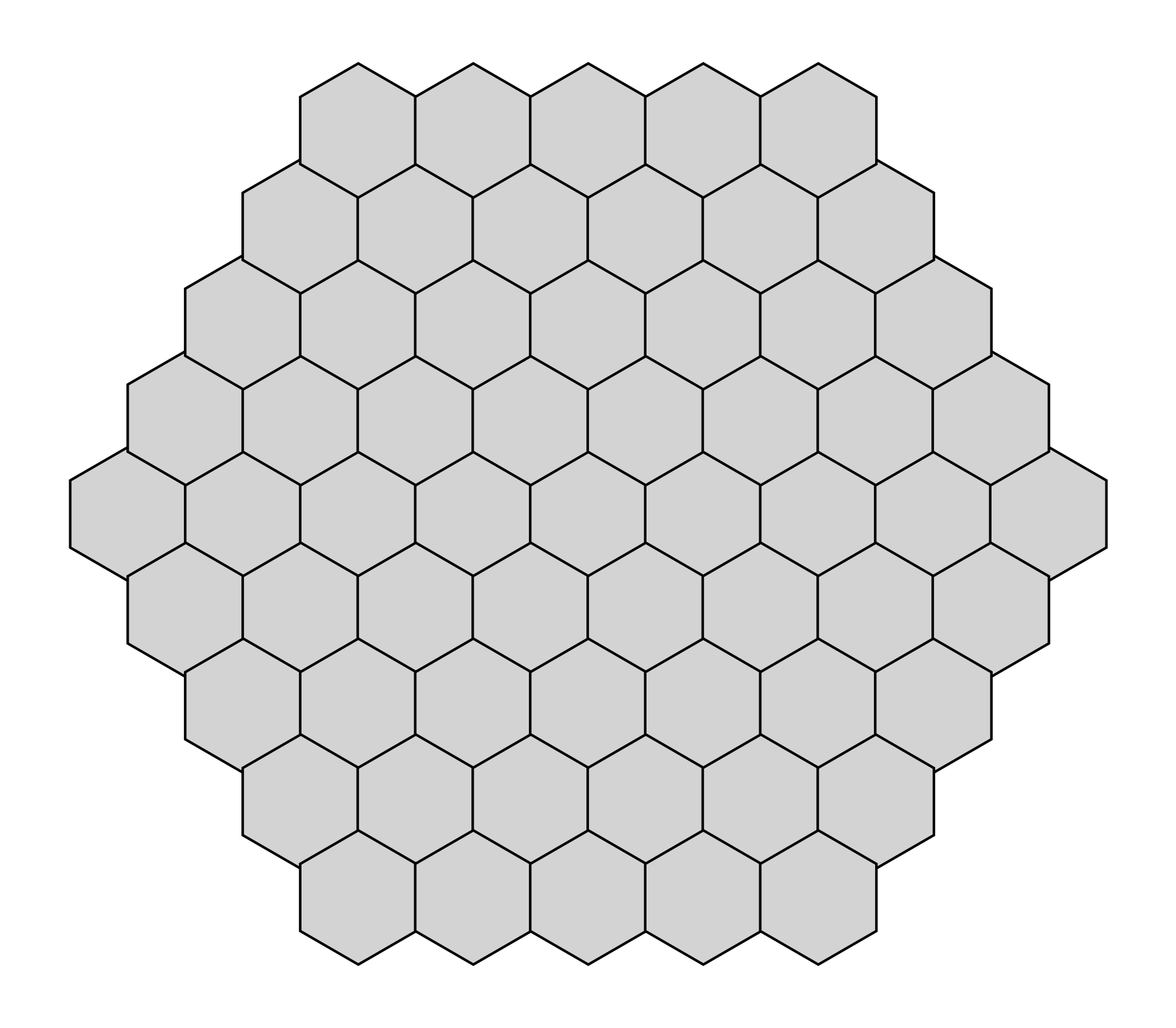
Tutte le celle inizialmente sono spente e la regola per accenderle è semplice:
Una cella si accende se e solo se è circondata da 3 celle già accese.
La domanda è:
Qual è il numero minimo di celle da accendere inizialmente e dove devono essere posizionate affinché dopo l’n-esima iterazione illumini tutte le celle?
Clicca qui per la soluzione
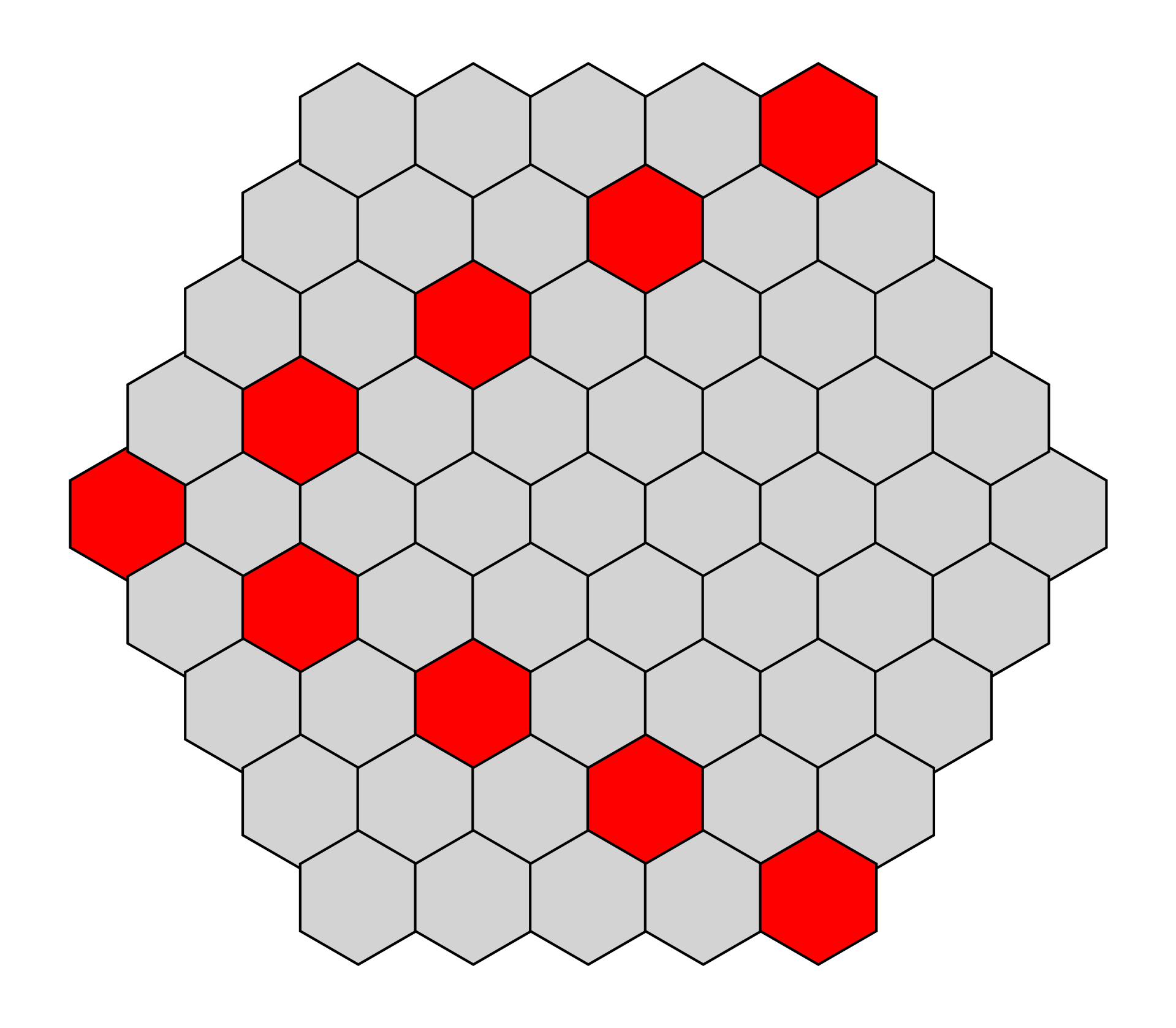
Le soluzioni a questo quesito sono molteplici, e sopra ne ho mostrata una delle possibili.
Ciò che colpisce subito è il fatto che il numero minimo di celle necessario per illuminare l’intero esagono è 9.
Questo numero non è casuale: nasce dalla regola delle tre celle accese contigue. Ogni cella può accendersi solo se circondata da tre celle già illuminate, e da questa semplice regola emerge un vincolo geometrico più profondo: l’invariante del perimetro.
Infatti qualsiasi sia la dimensione del esagono, la soluzione sarà sempre il numero di celle tale che il perimetro delle celle sia uguale al perimetro del esagono.
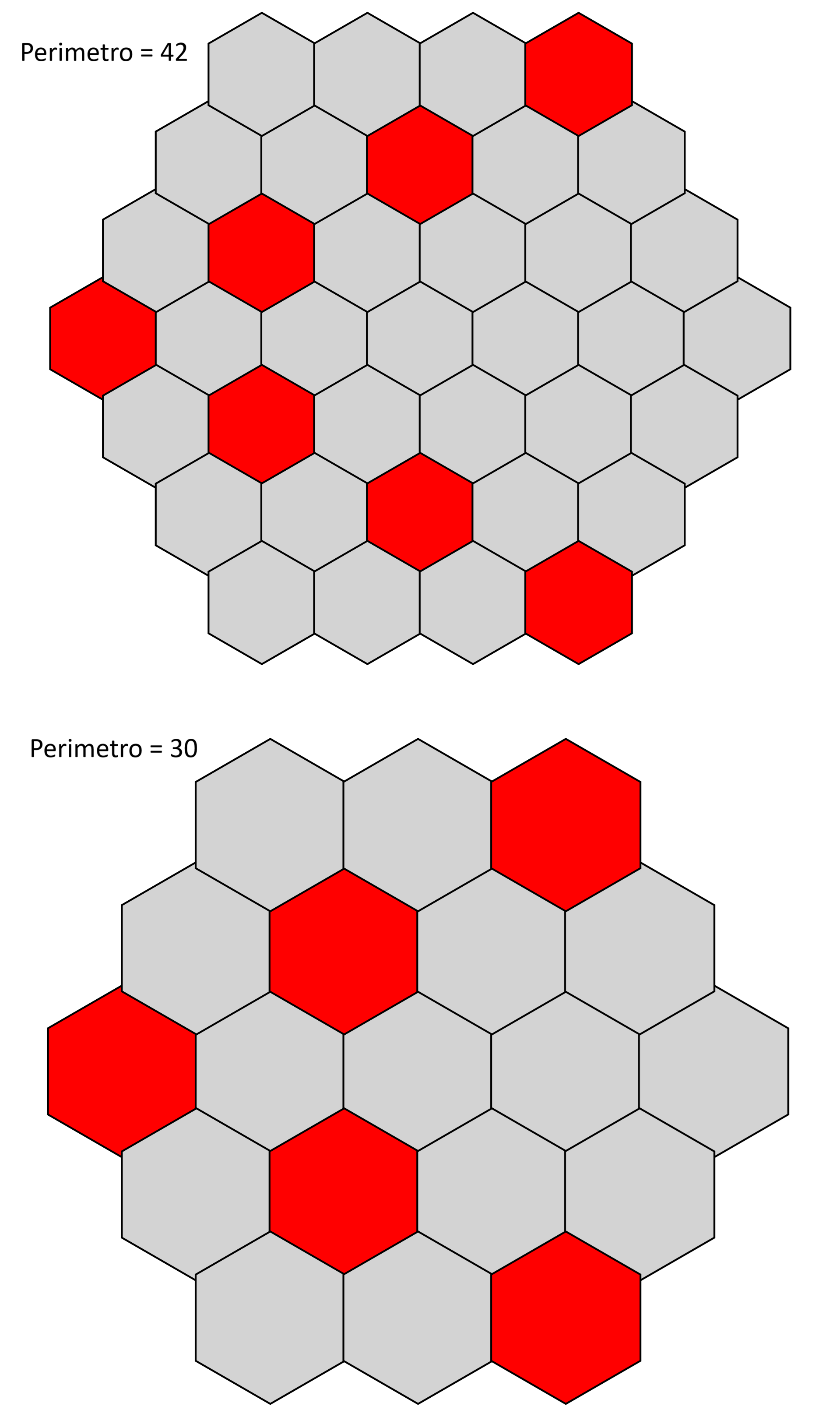
In altre parole, affinché una configurazione iniziale di celle accese sia realmente in grado di propagare la luce a tutto l’esagono, il perimetro calcolato dalle celle inizialmente accese deve coincidere con il perimetro dell’esagono grande.
Per l’esagono in questione, il perimetro misura 54 lati. Solo accendendo 9 celle non contigue si riesce a ottenere questa corrispondenza (poiché ogni esagonino ha 6 lati e $9 \cdot 6 = 54$).
La condizione necessaria e sufficiente affinché l’intero esagono si illumini è che la disposizione iniziale delle celle accese abbia un perimetro pari a quello dell’esagono grande. Il numero minimo di celle per soddisfare questa condizione è quindi 9, distribuite in modo da non essere contigue.